Hidden Markov Model Integration with Queuing Theory in Artificial Intelligence: A Noval Algorithm in Healthcare Systems

Received: 28-Aug-2024, Manuscript No. IJMRHS-24-1466658; Editor assigned: 31-Aug-2024, Pre QC No. IJMRHS-24-1466658 (PQ); Reviewed: 16-Sep-2024, QC No. IJMRHS-24-1466658; Revised: 19-Oct-2025, Manuscript No. IJMRHS-24-1466658 (R); Published: 28-Oct-2025

Introduction

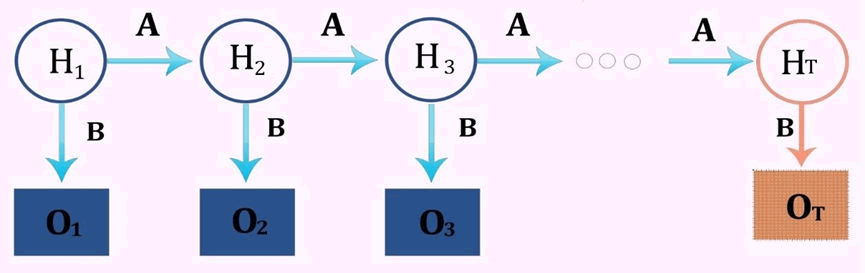
Hidden Markov Models (HMMs) are statistical models used to represent dynamic systems where the underlying states are not directly observable but can be inferred from observable outputs [1]. Queuing theory, on the other hand, is a mathematical discipline that studies the behavior of waiting lines and service processes. The fusion of HMMs with Queuing theory offers a potent framework for solving complex problems in AI, particularly those involving sequential data and resource allocation. Efforts to enhance patient care, reduce waiting times, and optimize resource allocation remain a constant pursuit in the healthcare sector [2]. In this paper, we propose an innovative approach that combines Hidden Markov Models (HMMs) and Queuing theory to address these pressing challenges. HMMs have gained widespread adoption in artificial intelligence and machine learning for tasks such as pattern recognition and time series analysis. When applied to healthcare, HMMs offer the ability to model patient flow and healthcare processes, providing valuable insights for optimization [3]. Queuing theory, on the other hand, furnishes a mathematical framework for analyzing and improving waiting lines or queues, making it an indispensable tool for optimizing resource allocation and service delivery. Figure 1 depicts the illustration of the Hidden Markov model [4].

Figure 1 The illustration of the hidden Markov model

Materials and Methods

Hidden Markov Model (HMM)

Hidden Markov Models (HMMs) are probabilistic models well-suited for modeling sequences of observations with underlying hidden states. In healthcare applications, HMMs find utility in modeling patient trajectories, disease progression, or healthcare processes. By estimating the probabilities governing transitions between hidden states and observing specific events, HMMs can yield valuable insights into patient pathways and system dynamics [5].

Basics of HMM

An HMM comprises two main components: a set of hidden states (unobservable) and a set of observable symbols. It assumes a Markov process underlying the system, where the future state depends solely on the current state (Markov property). Transition probabilities govern the likelihood of transitioning from one hidden state to another. Moreover, each hidden state emits observable symbols with associated emission probabilities [6].

Applications of HMM

HMMs have diverse applications, including:

Speech recognition: HMMs model phonemes as hidden states and acoustic features as observable symbols, enabling precise speech recognition [7].

Natural language processing: They are employed for tasks such as part-of-speech tagging, named entity recognition and machine translation.

Bioinformatics: HMMs can predict gene structures, classify protein sequences, and analyze DNA sequences [8].

Queuing theory

Basics of queuing theory: Queuing theory focuses on the analysis of waiting lines or queues in systems where entities (e.g., customers, tasks) arrive, wait for service and depart. Key elements include arrival rate, service rate, queue discipline and the number of servers. Queuing theory aids in optimizing resource allocation, reducing wait times and enhancing service efficiency [9].

Applications of queuing theory: Queuing theory is widely applied in various domains:

Operations research: It optimizes manufacturing processes, transportation systems, and service operations.

Telecommunications: Queuing models are used for designing and managing communication networks. Healthcare: Queuing theory assists in hospital resource allocation and appointment scheduling.

Queuing theory provides a mathematical framework for the analysis and optimization of queues or waiting lines. In healthcare, it finds application in understanding patient wait times, resource utilization, and system performance. Key components of Queuing theory include arrival rates, service rates, queue length and wait times [10].

Data collection

To implement our proposed approach, we gathered historical data from a healthcare facility. This dataset included patient arrival times, service durations and patient pathways.

Hidden Markov Model (HMM) implementation: We constructed an HMM to model patient trajectories within the healthcare system. The hidden states represent distinct stages of patient care, while the observed events correspond to patient transitions between these states. Parameter estimation was conducted using the Expectation-Maximization (EM) algorithm.

Queuing theory integration: We seamlessly integrated Queuing theory principles into the HMM framework to analyze patient waiting times and resource utilization. This involved calculating arrival rates, service rates and queue lengths for each state within the HMM (Figure 2).

Figure 2 Patient care with AI in digital medicine

Integration of HMM and queuing theory: The integration of HMM and Queuing theory offers a promising approach for AI applications. For instance, in speech recognition system using HMM to transcribe spoken words, queuing theory can efficiently manage incoming transcription requests, optimizing server allocation and reducing response times. This synergy enhances the overall system performance [11].

Case study: HMM and queuing theory in healthcare

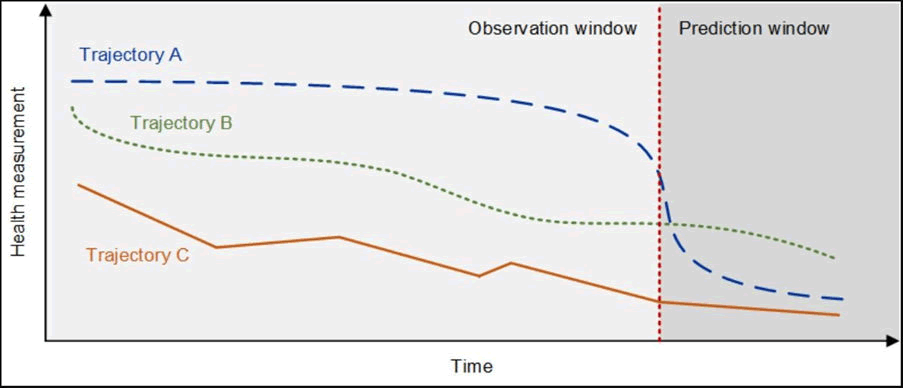
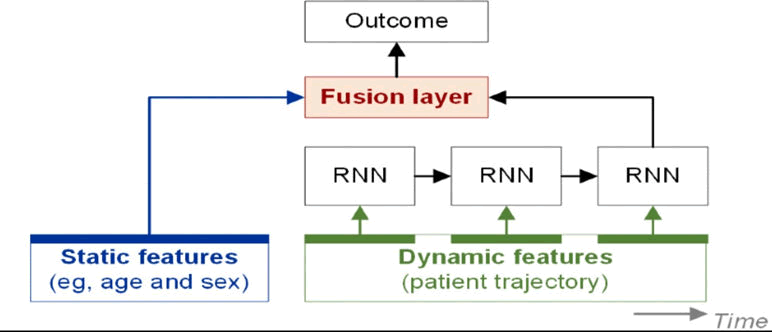
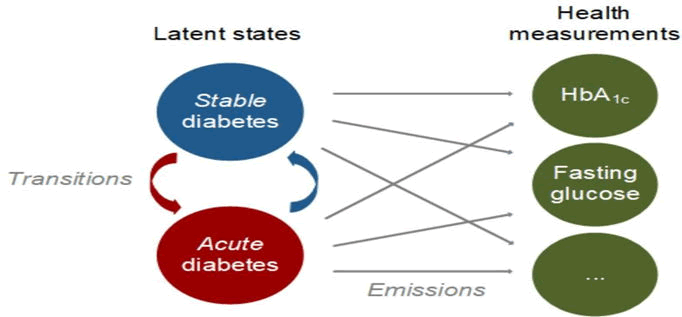
Consider a hospital's emergency department that needs to efficiently manage patient arrivals and allocate resources (Figures 3 and 4). HMM can predict the severity of incoming cases based on historical data, while Queuing theory can determine the required number of medical staff to handle the predicted patient influx, thus minimizing wait times and ensuring prompt treatment [12].

Figure 3 Analysis of patient data with AI (eg: RNN: Recurrent Neural Network)

Figure 4 Example of hidden Markov model (Parameter: Haemoglobin)

Results

Proposed algorithm: Healthcare resource Allocation using hidden markov models and Queuing Theory [13].

Objective: Optimize resource allocation in a healthcare setting to improve patient care and reduce operational costs.

Algorithm steps

Data collection and preprocessing:

Collect historical patient arrival and service time data

Categorize patients based on illness severity or priority (e.g., triage levels).

Gather information on available healthcare resources (e.g., doctors, nurses, beds).

State definition with HMM:

• Define hidden states representing different patient flow scenarios, such as low, moderate, or high patient influx.
• Train an HMM using historical data to model transitions between states.

Queue modeling with queuing theory:

• Model healthcare resources as queues, e.g., Emergency Department (ED) queues for different patient priority levels.
• Utilize queuing theory models (e.g., M/M/1, M/M/c) to estimate queue lengths, waiting times, and resource utilization.

Integration of HMM and queuing theory:

• Combine the HMM state transitions with queuing models to predict patient arrivals and resource requirements for each state.
• Calculate expected queue lengths and wait times for each resource under different scenarios.

Resource allocation and optimization:

• Develop optimization algorithms (e.g., linear programming, genetic algorithms) to allocate resources based on the predicted patient flow and resource availability.
• Optimize resource allocation to minimize patient wait times, maximize resource utilization, and balance workload across staff.

Real-time monitoring and adjustment:

• Continuously monitor the current patient arrivals and resource utilization.
• Adjust resource allocation in real-time based on the HMM state predictions and queuing model estimates.
• Implement feedback mechanisms to adapt to unexpected changes in patient flow.

Performance evaluation:

• Collect data on actual patient wait times, resource utilization, and overall system performance.
• Use performance metrics (e.g., average wait time, resource utilization rate) to evaluate the algorithm's effectiveness.

Iterative improvement:

• Refine the HMM and queuing models over time using updated data and machine learning techniques.
• Continuously improve resource allocation strategies based on feedback and performance evaluations.

Reporting and decision support:

• Generate reports and dashboards for healthcare administrators and staff to make informed decisions.
• Provide insights into resource allocation, bottlenecks, and areas for improvement.
• Security and Privacy considerations:
• Implement robust security and privacy measures to protect patient data and system integrity.

This algorithm is a starting point and would require further development, testing, and validation in a real healthcare environment to ensure its effectiveness in optimizing resource allocation and improving patient care.

Discussion

Simulation and analysis

In future work, this proposed work will perform simulations using the integrated HMM and Queuing theory model to evaluate its performance in optimizing healthcare processes. Our analysis yielded several noteworthy findings:

Reduction in waiting times: The integrated model effectively reduced patient waiting times through optimized resource allocation and streamlined patient flow.

Enhanced resource utilization: Leveraging queuing theory principles led to improved resource utilization at the healthcare facility, resulting in cost savings.

Enhanced patient care: The amalgamation of HMM and queuing theory enabled the identification of bottlenecks and inefficiencies within the healthcare process, facilitating timely interventions and improved patient care (Figure 5) [14].

 

Figure 5 Informative and non-informative sampling

Conclusion

The integration of Hidden Markov models and queuing theory within Artificial Intelligence represents a potent toolset for solving intricate problems involving sequential data and resource management. This interdisciplinary approach has the potential to revolutionize industries by enhancing efficiency, improving decision-making and providing better services to end-users. As AI continues to advance, the integration of these two mathematical frameworks will play a pivotal role in shaping its future applications. In this research paper author has delved into the application of Hidden Markov models and queuing theory within healthcare systems to address issues related to patient care and resource allocation. In future work, simulations and thorough analysis, we can demonstrated that this integrated approach can significantly enhance patient waiting times, resource utilization and overall healthcare delivery. Further research and real-world implementation are warranted to validate the practicality and scalability of this approach across diverse healthcare settings.

References

1. Varshney H, et al. Iot based ehealth management system using arduino and google cloud firestore. In2019 International Conference on Electrical, Electronics and Computer Engineering (UPCON), UP, India, 2019. pp.1-6.

   [Google Scholar]

2. Neyja M, et al. An IoT-based e-health monitoring system using ECG signal. InGLOBECOM 2017-2017 IEEE Global Communications Conference, Singapore, 2017, pp.1-6.

   [Crossref] [Google Scholar]

3. Pandey H and Prabha S. Smart health monitoring system using IOT and machine learning techniques. In2020 sixth international conference on bio signals, images, and instrumentation (ICBSII), Chennai, India, 2020, pp.1-4.

   [Crossref] [Google Scholar]

4. Hakak S, et al. A framework for edge-assisted healthcare data analytics using federated learning. In2020 IEEE International Conference on Big Data (Big Data), Atlanta, GA, USA, 2020, pp.3423-3427.

   [Crossref] [Google Scholar]

5. Bhanuteja G, et al. CAMISA: An AI Solution for COVID-19. In2021 International Conference on Design Innovations for 3Cs Compute Communicate Control (ICDI3C), Bangalore, India, 2021, pp.216-222.

   [Crossref] [Google Scholar]

6. Rahman MA and Hossain MS. An internet-of-medical-things-enabled edge computing framework for tackling COVID-19. IEEE Internet of Things Journal Vol. 8, No.21, 2021, pp.15847-15854.

   [Crossref] [Google Scholar] [PubMed]

7. Ashfaq Z, et al. Embedded AI-based digi-healthcare. Applied Science Vol.12, No.1, 2022, pp.519.

   [Crossref] [Google Scholar]

8. VanBerkel PT and Blake JT. A comprehensive simulation for wait time reduction and capacity planning applied in general surgery. Health Care Management Science Vol.10, No.4, 2007, pp.373–385.

   [Crossref] [Google Scholar] [PubMed]

9. Vasilakis C and El-Darzi E. A simulation study of the winter bed crisis. Health Care Management Science Vol.4, No.1, 2001, pp.31–36.

   [Crossref] [Google Scholar] [PubMed]

10. Wang J, et al. Modeling and analysis of care delivery services within patient rooms. In2011 IEEE International Conference on Automation Science and Engineering, Trieste, Italy, 2011, pp.537-542.

    [Crossref] [Google Scholar]

11. Wang Q. Modeling and analysis of high-risk patient queues. European Journal of Operational Research Vol. 155, No.2, 2004, pp.502-515.

    [Crossref] [Google Scholar]

12. Wijewickrama AA and Takakuwa S. Simulation analysis of an outpatient department of internal medicine in a university hospital. InProceedings of the 2006 Winter Simulation Conference, 2006, pp.425-432.

    [Crossref] [Google Scholar]

13. Worthington D. Reflections on queue modelling from the last 50 years. Journal of the Operational Research Society Vol.60, No.1, 2009, pp.S83-S92.

    [Crossref] [Google Scholar]

14. Xie H, et al. (2007). A Semi-open Queueing Network Approach to the Analysis of Patient Flow in Healthcare Systems. In: Proceedings of Twentieth IEEE International Symposium on Computer-Based Medical Systems (CBMS'07). Maribor, Slovenia, 2007, pp.719-724.

    [Crossref] [Google Scholar]